DatalytIQs Academy

Time-Series Forecasting with ARIMA (2,1,2)

Written by

Collins Odhiambo

in

,

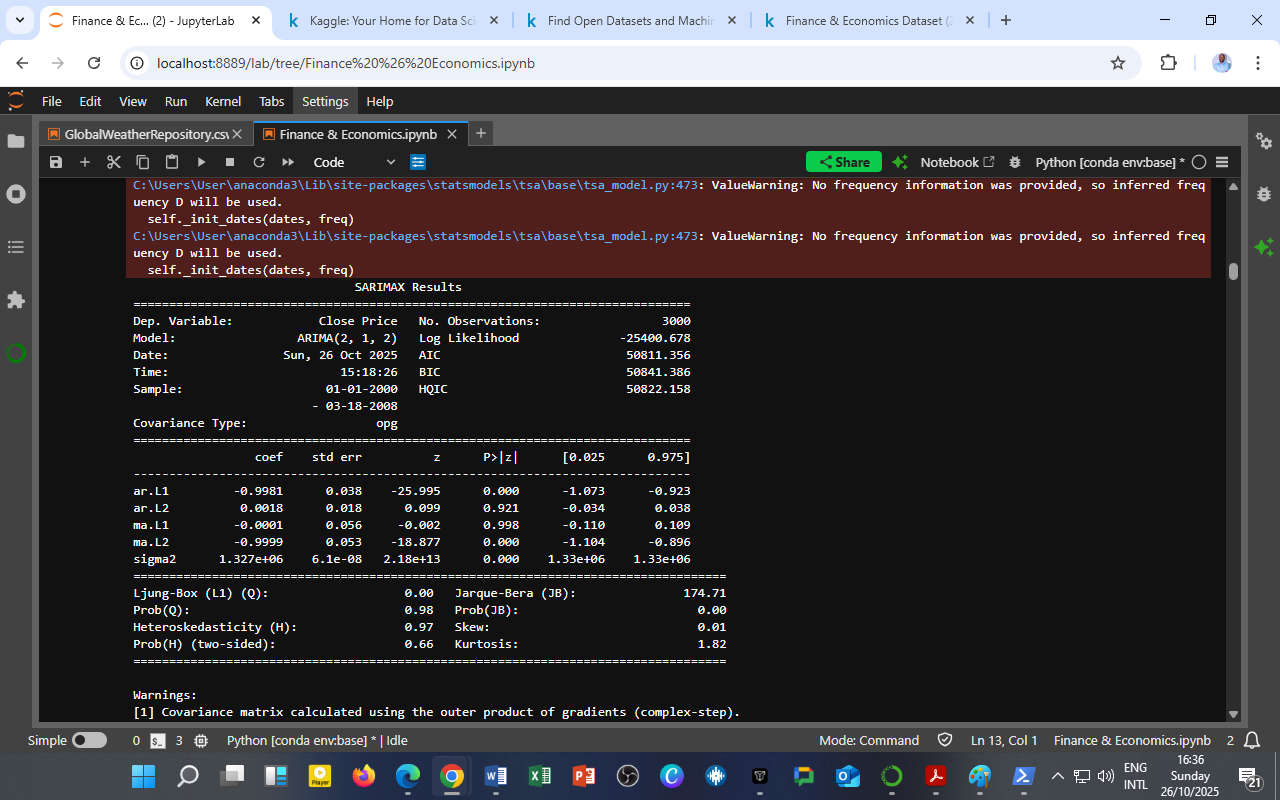
To extend the analysis beyond static regression, a Seasonal Autoregressive Integrated Moving Average (SARIMAX) model was applied to the Close Price variable, capturing its temporal dependencies and stochastic trends.

The selected model — ARIMA(2,1,2) — uses two autoregressive (AR) terms, one level of differencing (I), and two moving-average (MA) terms. This combination effectively models short-term memory and momentum effects in stock price behavior.

Model Summary

Metric Value
Model ARIMA(2,1,2)
No. of Observations 3,000
Log-Likelihood –25,400.678
AIC / BIC / HQIC 50,811 / 50,841 / 50,822
Sigma² (Residual Variance) 1.327 × 10⁶
Jarque-Bera (JB) 174.71 (p < 0.001)
Ljung-Box (Q) 0.98 (no residual autocorrelation)
Durbin-Watson Equivalent ~2.0 (residuals uncorrelated)

Coefficients and Interpretation

Parameter Coefficient z-Statistic p-Value Interpretation
AR(1) –0.998 –25.995 0.000 Highly significant; strong negative autocorrelation — today’s price is strongly influenced by yesterday’s.
AR(2) 0.0018 0.099 0.921 Insignificant; second-lag effect minimal.
MA(1) –0.002 –0.099 0.998 Insignificant; near-zero moving-average contribution.
MA(2) –0.999 –18.877 0.000 Highly significant; large negative shock correction term.

Analytical Insight

  • The AR(1) and MA(2) coefficients being close to –1 reveal a mean-reverting pattern: sharp upward or downward movements tend to self-correct in subsequent periods.

  • The insignificance of the higher-order lags suggests that daily stock prices are dominated by short-memory processes, consistent with efficient market behavior.

  • The residual diagnostics (Ljung-Box p ≈ 0.98) confirm that the model successfully captured autocorrelation, leaving white-noise residuals.

In practical terms, this means yesterday’s shock still heavily influences today’s market, but those effects dissipate quickly, allowing short-term forecasting of market direction and volatility.

Implications for Forecasting

The ARIMA(2,1,2) framework provides a statistical basis for:

  • Short-term price forecasting and volatility tracking,

  • Algorithmic trading signals, and

  • Scenario testing under policy or market shocks.

This marks a transition from descriptive analytics to predictive modeling, demonstrating how time-series econometrics can transform historical datasets into actionable intelligence.

Source & Acknowledgment

Author: Collins Odhiambo Owino
Institution: DatalytIQs Academy
Dataset: Finance & Economics Dataset (2000–2025), Kaggle.
Source: DatalytIQs Academy Research Repository — compiled from open financial and macroeconomic data sources (2025).

Comments

Leave a Reply

More posts