When Mathematics Meets Aesthetics: Tessellations as a Precise Tool for Solving Complex Problems

Mathematics is often celebrated for its precision, logic, and rigor—but beneath its formal symbols lies a world of breathtaking beauty and design. In a recent study, mathematicians from Freie Universität Berlin have shown that the geometric elegance of tessellations—the art of tiling a surface with perfectly fitting shapes—can do far more than please the eye. It can solve some of the most challenging mathematical problems in analysis, physics, and engineering.

Published in the journal Applicable Analysis, the study “Beauty in/of Mathematics: Tessellations and Their Formulas” by Professor Heinrich Begehr and Dajiang Wang merges artistry with mathematical precision. It reveals how intricate geometric patterns can serve as analytical frameworks for solving boundary value problems, such as the Dirichlet and Neumann problems—cornerstones of mathematical physics.

The Parqueting-Reflection Principle: Beauty with Structure

At the heart of this research lies the parqueting-reflection principle—a mathematical technique that uses repeated reflections of geometric shapes across their edges to fill a plane seamlessly, with no gaps or overlaps. The resulting symmetry mirrors the enchanting works of M.C. Escher, but with an added layer of analytical depth.

“Beauty in mathematics is not only an aesthetic notion,” explains Professor Begehr, “but something with structural depth and efficiency.”

By reflecting geometric figures—such as circular polygons or Schweikart triangles—mathematicians can develop explicit integral representations of functions within those tiled regions. These representations are then used to construct kernel functions (such as Green, Neumann, and Schwarz kernels) that provide elegant, computable solutions to otherwise complex differential equations in physics and engineering.

A Legacy of Berlin’s Mirror Tilings

This study continues a two-decade research tradition at Freie Universität Berlin’s Institute of Mathematics, where Begehr’s group has been exploring what they call the “Berlin mirror tilings.”

This approach stems from the unified reflection principle first proposed by Hermann Amandus Schwarz (1843–1921)—a Berlin mathematician whose work laid the foundation for modern complex analysis. By reflecting circular polygons (shapes bounded by straight lines and circular arcs) repeatedly, mathematicians can tile entire planes or disks, forming patterns that are both visually captivating and mathematically exact.

“Mathematicians once used a three-part vanity mirror to produce endless reflections,” Begehr notes humorously. “Today, we achieve the same result using iterative computer programs—enhanced by precise formulas from complex analysis.”

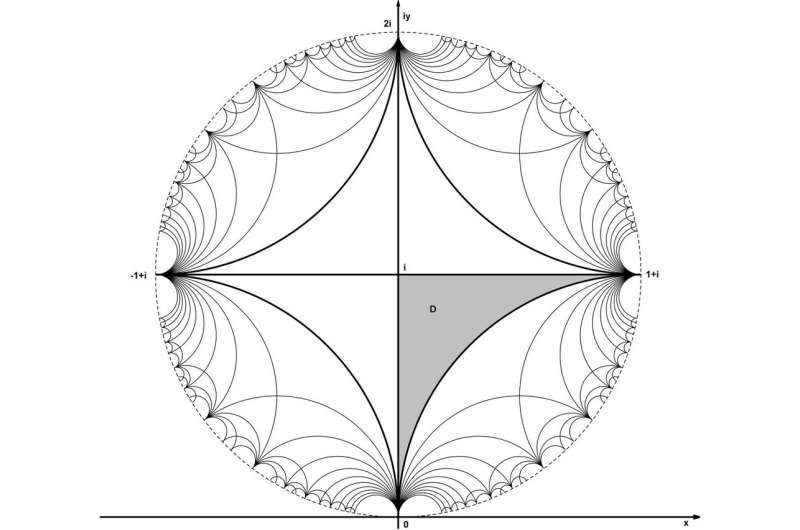
Schweikart Triangles: Hyperbolic Beauty

The research also explores tessellations in hyperbolic geometries, where traditional Euclidean rules no longer apply. In this curved mathematical space, used in theoretical physics and models of spacetime, the team works with Schweikart triangles, named after the 19th-century scholar Ferdinand Kurt Schweikart.

These unique triangles, defined by one right angle and two zero angles, can be reflected infinitely within a circular disk to produce intricate hyperbolic tessellations. The patterns are mesmerizing, resembling stained-glass windows or fractal spirals—but they also have analytical value.

In 2024, Begehr demonstrated this principle’s power by constructing a harmonic Green function for a Schweikart triangle in hyperbolic space, published in Complex Variables and Elliptic Equations. His findings revealed that even in the warped realms of hyperbolic geometry, mathematical beauty maintains its precision and purpose.

Where Art, Mathematics, and Technology Intersect

What makes this work so compelling is its reach beyond pure mathematics. The parqueting-reflection principle offers inspiration for architecture, design, and computer graphics, where symmetry and form play key roles. As co-author Dajiang Wang notes:

“We hope our results resonate not only in pure mathematics and physics, but also inspire ideas in fields like architecture and digital visualization.”

By merging analytical formulas with geometric creativity, this research bridges two worlds often seen as opposites: mathematics as logic and art as expression. In truth, the two share the same heartbeat—pattern, proportion, and precision.

Mathematics as a Visual Science

This study reminds us that mathematics is more than abstraction; it’s a visual science. Its symbols are not just tools for calculation, but expressions of symmetry, motion, and infinite beauty. With modern computational graphics, these visual insights can now be rendered with stunning clarity—transforming equations into art and geometry into algorithms.

At DatalytIQs Academy, such discoveries exemplify our philosophy: that learning mathematics is not only about solving problems but about seeing the patterns that structure reality itself.

Citation & Acknowledgments

Source Article:
Freie Universität Berlin (2025). “When mathematics meets aesthetics: Tessellations as a precise tool for solving complex problems.”
Published on Phys.org, written by Krystal Kasal.
Edited by: Lisa Lock
Reviewed by: Robert Egan
Original Study: Heinrich Begehr & Dajiang Wang, “Beauty in/of Mathematics: Tessellations and Their Formulas,” Applicable Analysis (DOI: 10.1080/00036811.2025.2510472).

Author: Collins Odhiambo — DatalytIQs Academy Mathematics & Innovation Blog
Category: Mathematical Physics & Geometry