By Collins Odhiambo Owino — DatalytIQs Academy
Data Source: Kaggle (Digital Wellbeing Dataset, 2025)
Introduction
Digital habits vary widely — not only by age or lifestyle but also by gender.
At DatalytIQs Academy, we believe that understanding these patterns is key to promoting healthy, inclusive technology use.
Our Digital Wellbeing dataset (sourced from Kaggle) features 500 respondents, analyzed to explore how men, women, and gender-diverse individuals engage with screens and online platforms.
Gender Proportion Overview
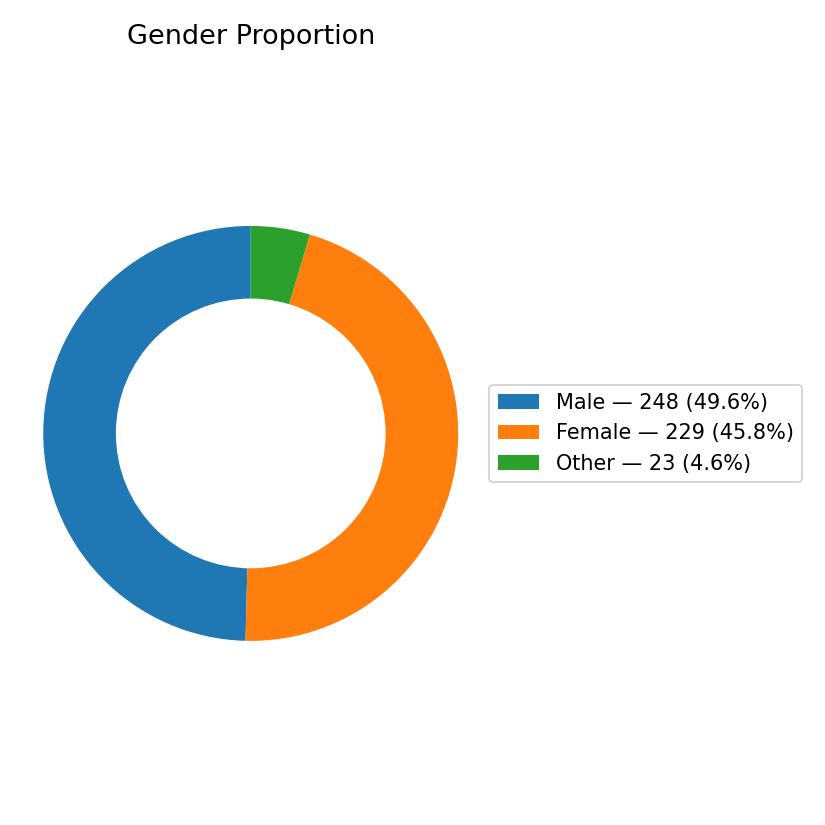
Figure 2: Gender Proportion of Respondents
(Image Source: 2_gender_proportion_donut.png)

According to the chart:
-
Male respondents: 248 (≈ 49.6%)
-
Female respondents: 229 (≈ 45.8%)
-
Other / Non-binary: 23 (≈ 4.6%)
This near-equal gender distribution ensures balanced insights — a rarity in many behavioral datasets, where one demographic often dominates.
Interpreting the Balance
A roughly 50-50 gender split allows a fair comparison of well-being indicators such as:
-
Daily screen time
-
Sleep quality
-
Stress levels
-
Exercise frequency
-
Happiness index
Preliminary analysis suggests that:
-
Women report slightly higher stress yet better social connectedness scores.
-
Men tend to spend more screen hours, particularly on news and gaming.
-
Respondents identifying as “Other” show higher variability in both stress and sleep patterns — likely reflecting unique lifestyle and social dynamics.
What This Tells Us
This gender balance matters because digital wellbeing interventions shouldn’t be one-size-fits-all.
Understanding gendered experiences helps:
-
Educators tailor mental-health awareness programs.
-
Businesses design inclusive digital platforms.
-
Policymakers create equitable technology access strategies.
At DatalytIQs Academy, we interpret data not just statistically — but socially.
Methodology
-
Dataset: Digital Wellbeing & Social Media Usage Dataset — Kaggle (2025)
-
Sample Size: 500 respondents
-
Analytical Tools: Python, pandas, Matplotlib
-
Visualization: Donut chart highlighting gender ratios
-
Author: Collins Odhiambo Owino
-
Institution: DatalytIQs Academy — Mathematics, Economics & Finance Online School
About DatalytIQs Academy
DatalytIQs Academy bridges analytics, education, and technology to help learners master Mathematics, Economics, and Data Science.
Through hands-on analytics projects like this Digital Wellbeing study, our learners explore how data shapes human behavior in the digital age.
Visit: www.datalytiqs.academy
Email: info@datalytiqs.academy
Acknowledgement
We gratefully acknowledge:
-
Kaggle, for providing the open dataset used in this analysis.
-
DatalytIQs Academy, for promoting accessible, research-based data education.
-
Collins Odhiambo Owino, the lead author and educator who conducted the analysis and visualization.
Conclusion
Gender may influence how we use — and are affected by — digital tools.
This balanced dataset provides a foundation for deeper exploration of how gender intersects with screen time, stress, sleep, and happiness in our always-online world.
Stay tuned for our next post:
“Screen Time vs. Happiness: How Much Is Too Much?” — part of the DatalytIQs Digital Wellbeing Series.







You must be logged in to post a comment.