DatalytIQs Academy

Are Earthquakes Random?

Written by

Collins Odhiambo

in

, , , ,

Overview

Earthquakes are often assumed to occur randomly, independent events following a Poisson process, much like radioactive decay or raindrops falling on a roof.
However, real-world seismic activity can behave very differently due to tectonic interactions, aftershock sequences, and periodic stress release.

This analysis, conducted using the Global Earthquake–Tsunami Risk Assessment Dataset (2001–2022), tests whether global earthquake inter-event times follow a Poisson process or show evidence of temporal clustering.

The Statistical Test

The Kolmogorov–Smirnov (K–S) test was used to compare the observed inter-event time distribution with a theoretical exponential distribution expected from a Poisson process.

Results:

Fitted exponential mean (λ⁻¹): 6.5639 months
K–S Statistic: 0.2057
P-value: 0.000000

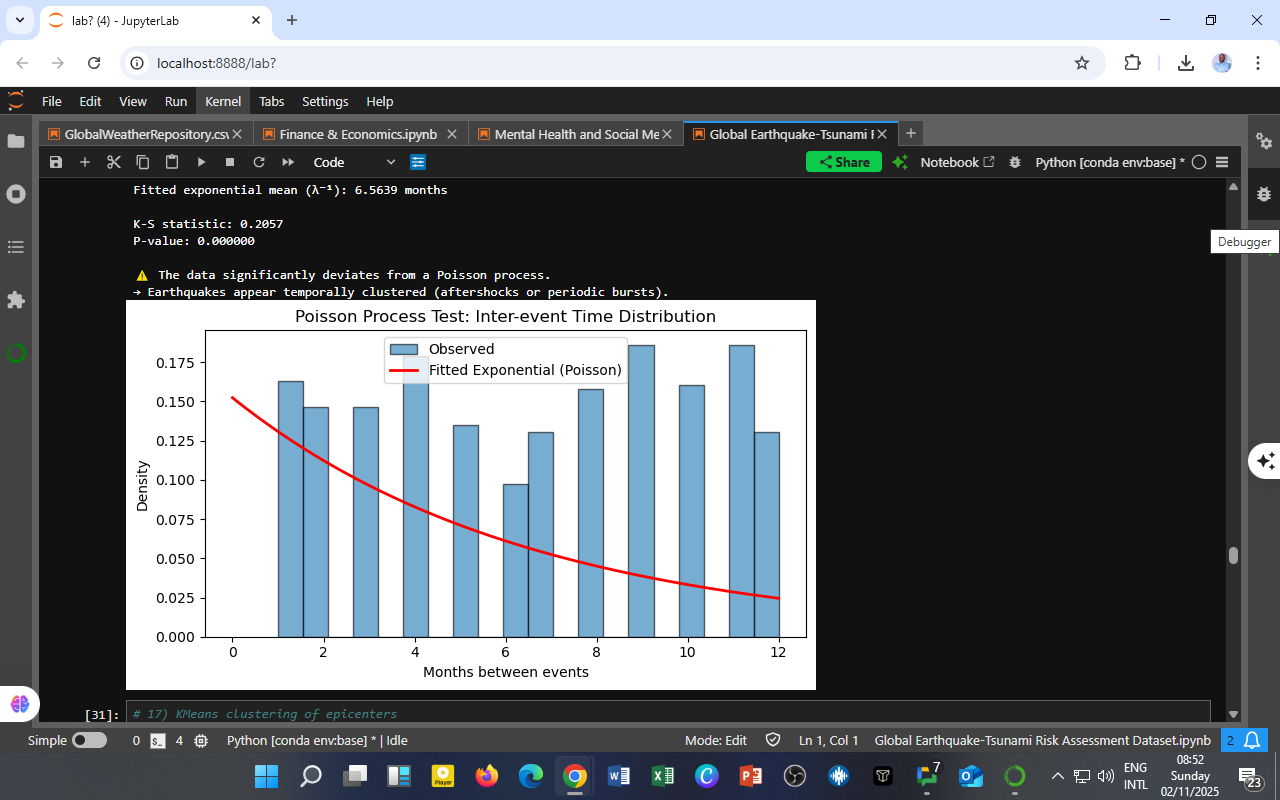
Visualization — Poisson Process Test

Figure Description

The histogram (blue bars) represents the observed time intervals between successive global earthquakes.
The red curve shows the expected exponential decay if earthquakes followed a purely random Poisson process.

Interpretation

  • The very low p-value (< 0.001) indicates that the observed data significantly deviates from the random (Poisson) model.

  • This suggests that earthquakes do not occur independently over time; instead, they tend to cluster.

  • Such clustering can be explained by:

    • Aftershock sequences following major quakes,

    • Regional stress transfer triggering nearby faults,

    • Periodic bursts of tectonic activity in subduction zones.

“The Earth doesn’t shake at random — it pulses with cycles of stress and release.”

Key Findings

  • Mean inter-event time ≈ 6.56 months, meaning that globally, a significant quake tends to occur roughly twice a year.

  • The Poisson assumption fails, confirming temporal dependency between events.

  • Earthquakes occur in bursts — intense periods of seismic activity followed by relative calm.

Implications for Research and Policy

  • Seismic Forecasting:
    Temporal clustering supports models like the Epidemic-Type Aftershock Sequence (ETAS), which better capture aftershock-triggered behavior.

  • Disaster Preparedness:
    Recognizing burst periods can help agencies enhance monitoring and communication immediately following major quakes.

  • Machine Learning Integration:
    Poisson-based assumptions may underperform; temporal clustering features can improve time-series and neural network forecasting of seismic events.

Acknowledgment

This analysis was performed by DatalytIQs Academy, a global platform for learning and applied research in Mathematics, Economics, and Earth Science Analytics.

Dataset: Global Earthquake–Tsunami Risk Assessment Dataset (2001–2022) — available on Kaggle.
Tools Used: Python | Pandas | Matplotlib | Scipy | JupyterLab

“At DatalytIQs Academy, we transform seismic data into insight — building resilience through science.”
— Collins Odhiambo Owino, Founder

Acknowledgment of Contributions:
This work gratefully acknowledges the open data contributors and scientific community on Kaggle, whose transparent sharing of seismic data continues to support global risk assessment and academic research.

Comments

Leave a Reply

More posts